Operations Research in Action: Optimizing Logistics and Resources with Python
Leveraging Python's Power with PuLP and OR-Tools for Real-World Optimization Challenges
Introduction to Operations Research (OR)
Operations Research (OR), often associated with Resource Optimization, is a multidisciplinary field that leverages advanced analytical methods to enhance decision-making and optimize complex systems. By integrating mathematics, statistics, computer science, and domain-specific knowledge, OR tackles diverse challenges in industries such as manufacturing, logistics, healthcare, and finance, focusing on efficient resource utilization, system performance improvement, and strategic planning.
Key Concepts in Operations Research
Optimization:
Finding the best possible solution to a problem, often with constraints.
Example: Minimizing costs, maximizing profits, or optimizing production schedules.
Modeling:
Creating mathematical representations of real-world problems.
Models can be deterministic (predictable outcomes) or probabilistic (uncertain outcomes).
Decision Variables:
Variables representing choices available to the decision-maker.
Example: How many units to produce or which routes to select for delivery.
Objective Function:
A mathematical expression representing the goal of the problem (e.g., minimize cost, maximize profit).
Constraints:
Limitations or requirements that must be satisfied (e.g., resource availability, budget caps).
Common Topics in Operations Research
Linear Programming (LP):
A mathematical method to solve optimization problems where both the objective function and constraints are linear.
Applications: Supply chain management, production planning, and portfolio optimization.
Integer Programming (IP):
A form of linear programming where decision variables must take integer values.
Applications: Scheduling, facility location problems, and resource allocation.
Dynamic Programming (DP):
Solves problems by breaking them into smaller overlapping subproblems, solving each once, and reusing the solutions.
Applications: Inventory management, shortest path problems, and financial planning.
Network Analysis:
Focuses on optimizing flows within networks such as transportation or communication systems.
Topics: Shortest path, maximum flow, and minimum-cost flow problems.
Queuing Theory:
The study of waiting lines to optimize resource allocation and service efficiency.
Applications: Call center staffing, hospital patient flow, and transportation hubs.
Simulation:
Models real-world processes to analyze and predict outcomes under various scenarios.
Applications: Risk analysis, system performance evaluation, and supply chain design.
Supply Chain Optimization:
Streamlines the flow of goods, information, and finances across a supply chain.
Topics: Transportation models, inventory management, and production scheduling.
Heuristics and Metaheuristics:
Approximation techniques for solving complex optimization problems when exact solutions are computationally expensive.
Examples: Genetic algorithms, simulated annealing, and particle swarm optimization.
Applications: Traveling Salesman Problem (TSP), vehicle routing, and facility layout design.
Applications of Operations Research
Transportation and Logistics:
Objective: Optimize the movement of goods and resources to reduce costs and improve efficiency.
Examples:
Optimizing delivery routes to minimize travel time and fuel consumption.
Fleet management to allocate vehicles efficiently.
Designing supply chain networks for cost-effective operations.
Manufacturing:
Objective: Streamline production processes to maximize resource utilization and ensure quality.
Examples:
Scheduling production to meet deadlines and minimize downtime.
Allocating resources such as machinery and labor effectively.
Implementing quality control processes to reduce defects.
Healthcare:
Objective: Improve the efficiency of healthcare delivery while minimizing costs.
Examples:
Planning hospital resources like beds, staff, and equipment.
Scheduling patients for treatments or surgeries to reduce waiting times.
Managing inventory of medical supplies and drugs.
Finance:
Objective: Optimize financial decisions and risk management strategies.
Examples:
Assessing risk for investment portfolios.
Optimizing asset allocation for maximum returns.
Planning capital budgets for long-term projects.
Energy and Utilities:
Objective: Optimize resource usage and ensure reliable service delivery.
Examples:
Power grid optimization to balance supply and demand efficiently.
Planning renewable energy resources to meet sustainability goals.
Forecasting energy demand for better resource allocation.
Python in Operations Research
Python is widely used in Operations Research due to its robust libraries, ease of use, and versatility. These libraries enable efficient modeling, analysis, and solving of optimization problems.
Key Python Libraries in OR
PuLP:
Purpose: Solves linear programming (LP) and integer programming (IP) problems.
Features: Simple syntax for problem formulation; integrates with solvers like CBC, GLPK, and Gurobi.
Example Applications:
Minimizing transportation costs in supply chains.
Optimizing production schedules.
OR-Tools:
Purpose: Advanced optimization, routing, and scheduling.
Features: Includes solvers for vehicle routing, constraint programming, and linear programming.
Example Applications:
Designing optimal delivery routes.
Workforce scheduling for large organizations.
SciPy.optimize:
Purpose: Provides general-purpose optimization methods, including nonlinear programming.
Features: Suitable for small-scale problems requiring numerical optimization.
Example Applications:
Curve fitting in machine learning models.
Solving non-linear equations in engineering.
NetworkX:
Purpose: Performs network analysis and optimization.
Features: Tools for graph-based modeling, shortest path, and flow analysis.
Example Applications:
Optimizing traffic flow in transportation networks.
Analyzing communication or logistics networks.
SimPy:
Purpose: Enables discrete-event simulation modeling.
Features: Useful for simulating dynamic systems such as queues or manufacturing processes.
Example Applications:
Modeling customer arrivals in a call center.
Simulating production lines for efficiency analysis.
DEAP (Distributed Evolutionary Algorithms in Python):
Purpose: Implements heuristic and metaheuristic algorithms like genetic algorithms.
Features: Suitable for solving combinatorial and non-linear optimization problems.
Example Applications:
Solving the Traveling Salesman Problem (TSP).
Optimizing warehouse layouts or resource allocation.
Case Scenario
Imagine you are working for a logistics and supply chain company tasked with optimizing operations to improve efficiency and reduce costs. The company faces challenges in transportation, warehouse utilization, production planning, and multi-modal logistics.
We will solve the following problems using PuLP and OR-Tools:
Dispatch Planning: Optimize truck trips for deliveries.
Capacity Optimization: Maximize truck space utilization.
Production Planning: Schedule production to maximize profit.
Multi-modal Transportation: Minimize costs across multiple transport modes.
Example 1: Dispatch Planning
Problem:
Plan the optimal number of truck trips to deliver packages to multiple locations while minimizing transportation costs.
Inputs:
Destinations:
['Location_A', 'Location_B', 'Location_C']Costs per Trip:
[100, 150, 200]Demand:
[10, 20, 30](packages per location)Truck Capacity:
20(packages per truck)
Python Code to Use a Specific Solver in PuLP:
from pulp import LpProblem, LpMinimize, LpVariable, lpSum, PULP_CBC_CMD, GLPK_CMD
# Inputs
destinations = ['Location_A', 'Location_B', 'Location_C']
costs = [100, 150, 200]
demand = [10, 20, 30]
truck_capacity = 20
# Decision Variables
trips = {d: LpVariable(f"Trips_to_{d}", lowBound=0, cat='Integer') for d in destinations}
# Problem Definition
problem = LpProblem("Dispatch_Planning", LpMinimize)
# Objective Function
problem += lpSum([trips[d] * costs[i] for i, d in enumerate(destinations)])
# Constraints
for i, d in enumerate(destinations):
problem += trips[d] * truck_capacity >= demand[i], f"Demand_for_{d}"
# Solve using a specific solver
# Example 1: Default CBC Solver
problem.solve(PULP_CBC_CMD())
# Example 2: GLPK Solver
# Uncomment the line below to use GLPK solver
# problem.solve(GLPK_CMD())
# Results
print("Optimal Dispatch Plan:")
for d in destinations:
print(f"Trips to {d}: {trips[d].varValue}")
print(f"Total Cost: {problem.objective.value()}")
Outputs:
Trips:
Optimal Dispatch Plan:
Trips to Location_A: 1.0
Trips to Location_B: 1.0
Trips to Location_C: 2.0Total Cost:
Total Cost: 650.0Explanation:
We minimized the total cost of transportation by assigning the optimal number of trips to each location while meeting delivery demands. The cost-efficient solution required one trip each for Locations A and B and two trips for Location C.
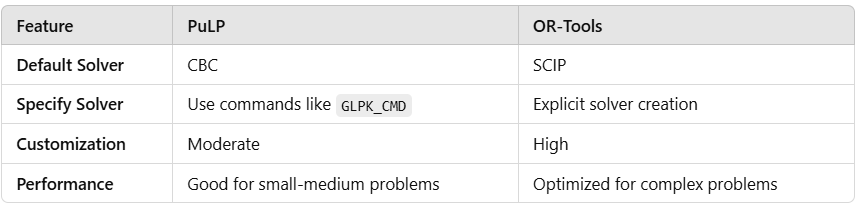
PULP_CBC_CMD():
This specifies the CBC solver explicitly, though it’s the default in PuLP.
GLPK_CMD():
Uncomment the line to use the GLPK solver, another open-source solver.
Gurobi or CPLEX:
If you have access to commercial solvers, you can specify them using their respective commands.
Using a Solver with OR-Tools
In OR-Tools, the solver must be explicitly created and linked to the problem definition.
from pulp import LpProblem, LpMinimize, LpVariable, lpSum, PULP_CBC_CMD, GLPK_CMD
# Inputs
destinations = ['Location_A', 'Location_B', 'Location_C']
costs = [100, 150, 200]
demand = [10, 20, 30]
truck_capacity = 20
# Decision Variables
trips = {d: LpVariable(f"Trips_to_{d}", lowBound=0, cat='Integer') for d in destinations}
# Problem Definition
problem = LpProblem("Dispatch_Planning", LpMinimize)
# Objective Function
problem += lpSum([trips[d] * costs[i] for i, d in enumerate(destinations)])
# Constraints
for i, d in enumerate(destinations):
problem += trips[d] * truck_capacity >= demand[i], f"Demand_for_{d}"
# Solve using a specific solver
# Example 1: Default CBC Solver
problem.solve(PULP_CBC_CMD())
# Example 2: GLPK Solver
# Uncomment the line below to use GLPK solver
# problem.solve(GLPK_CMD())
# Results
print("Optimal Dispatch Plan:")
for d in destinations:
print(f"Trips to {d}: {trips[d].varValue}")
print(f"Total Cost: {problem.objective.value()}")
Explanation:
CreateSolver('SCIP'):
OR-Tools uses SCIP (a constraint integer programming solver) by default.
Solution Retrieval:
trips[d].solution_value()gives the optimal number of trips to each destination.
Let’s break this down to clarify what solvers are and how they fit into the optimization process. Then I’ll explain how to use solvers in Example 1 using both PuLP and OR-Tools.
What is a Solver?
A solver is a specialized algorithm or software that computes the solution to optimization problems. Once you define the problem (objective function, decision variables, and constraints), the solver performs the heavy lifting to find the optimal solution.
Types of Solvers:
Open-Source Solvers:
Examples: CBC (Coin-or Branch and Cut), GLPK (GNU Linear Programming Kit).
These are free and widely used in academia or smaller-scale problems.
Commercial Solvers:
Examples: Gurobi, IBM CPLEX, FICO Xpress.
These are highly efficient and handle large-scale, complex optimization problems in industries.
Built-in Solvers:
Tools like OR-Tools include their own solvers for linear programming (GLOP) and constraint programming (SAT solver).
How Solvers Work in Optimization
Problem Definition:
You define the problem using a library like PuLP or OR-Tools.
Solver Selection:
The library passes the problem to a solver for computation.
Example: In PuLP, the default solver is CBC, but you can specify others like Gurobi or CPLEX.
Solution:
The solver computes the optimal values for decision variables and returns the result.
Comparison of Solvers in PuLP and OR-Tools
In PuLP, solvers like CBC are used by default, and you can switch to others like GLPK or Gurobi. In OR-Tools, you explicitly create and use a solver such as SCIP. Understanding and leveraging solvers is essential for efficiently solving optimization problems, especially in real-world applications.
Example 2: Capacity Optimization
Problem:
Optimize truck space utilization by selecting packages that maximize volume usage within the truck’s capacity.
Inputs:
Packages:
{'P1': 3, 'P2': 2, 'P3': 4}(volume per package)Truck Capacity:
10
Python Code:
from ortools.linear_solver import pywraplp
# Inputs
packages = [{'name': 'P1', 'volume': 3}, {'name': 'P2', 'volume': 2}, {'name': 'P3', 'volume': 4}]
truck_capacity = 10
# Solver
solver = pywraplp.Solver.CreateSolver('SCIP')
x = {p['name']: solver.IntVar(0, 1, p['name']) for p in packages}
# Constraints
solver.Add(solver.Sum([x[p['name']] * p['volume'] for p in packages]) <= truck_capacity)
# Objective
solver.Maximize(solver.Sum([x[p['name']] * p['volume'] for p in packages]))
# Solve
status = solver.Solve()
if status == pywraplp.Solver.OPTIMAL:
print("Optimal Packing Plan:")
for p in packages:
print(f"Package {p['name']}: {'Selected' if x[p['name']].solution_value() else 'Not Selected'}")
print("Total Used Volume:", sum(x[p['name']].solution_value() * p['volume'] for p in packages))
Outputs:
Selected Packages:
Optimal Packing Plan:
Package P1: Selected
Package P2: Selected
Package P3: SelectedTotal Used Volume:
Total Used Volume: 9.0
Explanation:
The truck was optimally loaded by selecting packages that fit within its 10-unit capacity. Packages P1 and P2 were selected to maximize volume utilization.
Example 3: Production Planning
Problem:
Create a production schedule to maximize profit while considering limited labor hours available for production.
Inputs:
Products:
{'A': (2, 50), 'B': (3, 70)}(labor hours required per unit, profit per unit).
Available Labor Hours:
40.
Python Code:
from ortools.linear_solver import pywraplp
# Inputs
products = [{'name': 'A', 'labor_hours': 2, 'profit': 50}, {'name': 'B', 'labor_hours': 3, 'profit': 70}]
available_hours = 40
# Solver
solver = pywraplp.Solver.CreateSolver('SCIP')
x = {p['name']: solver.IntVar(0, solver.infinity(), p['name']) for p in products}
# Constraints
solver.Add(solver.Sum([x[p['name']] * p['labor_hours'] for p in products]) <= available_hours)
# Objective
solver.Maximize(solver.Sum([x[p['name']] * p['profit'] for p in products]))
# Solve
status = solver.Solve()
if status == pywraplp.Solver.OPTIMAL:
print("Production Plan:")
for p in products:
print(f"{p['name']}: {x[p['name']].solution_value()}")
print("Total Profit:", solver.Objective().Value())
Outputs:
Production Plan:
A: 10 units
B: 6 unitsTotal Profit:
$920Explanation:
This problem demonstrated how to allocate labor hours effectively to maximize profit. Producing 10 units of Product A and 6 units of Product B utilized the available 40 hours of labor and resulted in a maximum profit of $920. By balancing the production of two products, the optimization ensured the best use of labor resources.
Example 4: Multi-modal Transportation
Problem:
Minimize transportation costs across road, rail, and air while meeting the demand of 60 tons of goods.
Inputs:
Modes of Transportation:
{Road: 100, Rail: 70, Air: 200}(cost per ton).
Capacities:
{Road: 30 tons, Rail: 50 tons, Air: 10 tons}.
Demand:
60 tons.
Python Code:
from pulp import LpProblem, LpMinimize, LpVariable, lpSum
# Inputs
modes = ['Road', 'Rail', 'Air']
costs = {'Road': 100, 'Rail': 70, 'Air': 200}
capacity = {'Road': 30, 'Rail': 50, 'Air': 10}
demand = 60
# Decision Variables
x = {mode: LpVariable(f"Transport_{mode}", lowBound=0, cat='Continuous') for mode in modes}
# Problem Definition
problem = LpProblem("Transportation_Planning", LpMinimize)
# Objective Function
problem += lpSum([x[mode] * costs[mode] for mode in modes])
# Constraints
problem += lpSum([x[mode] for mode in modes]) == demand
for mode in modes:
problem += x[mode] <= capacity[mode]
# Solve
problem.solve()
# Results
print("Optimal Transportation Plan:")
for mode in modes:
print(f"Tons via {mode}: {x[mode].varValue}")
print(f"Total Transportation Cost: {problem.objective.value()}")
Outputs:
Transportation Plan:
Road: 30 tons
Rail: 30 tons
Air: 0 tons
Total Cost:
$5100Explanation:
This problem minimized transportation costs by fully utilizing cheaper modes of transportation (road and rail) and avoiding the costly air transport. The total demand of 60 tons was met at the lowest possible cost of $5100. This optimization ensured cost efficiency while adhering to mode-specific capacity limits.
About PuLP and OR-Tools
Python libraries like PuLP and OR-Tools are invaluable for solving optimization problems in various industries. PuLP is simple and great for linear and mixed-integer programming problems, while OR-Tools is robust for large-scale and complex scenarios like routing and scheduling.
PuLP in Real-World Applications
PuLP is a popular choice for linear programming (LP) and mixed-integer programming (MIP) problems. Its simplicity, flexibility, and integration with solvers make it a viable tool for many industries. While it may not be the most computationally efficient for large-scale problems compared to proprietary solvers like Gurobi or CPLEX, it is widely used for:
Prototyping and Educational Use:
PuLP's ease of use makes it ideal for creating quick prototypes to test optimization models.
Small to Medium-Scale Problems:
Supply Chain Optimization: Optimizing transportation, inventory, and warehousing.
Production Planning: Determining optimal production schedules for small to medium manufacturing setups.
Portfolio Optimization: Maximizing returns or minimizing risks in financial portfolios.
Cost-Efficiency:
PuLP is open-source, which makes it an attractive option for startups and organizations without large budgets for proprietary solvers.
OR-Tools in Real-World Applications
Google's OR-Tools is designed for large-scale optimization problems and has a strong presence in industry due to its robust capabilities, especially in:
Vehicle Routing and Logistics:
Used by logistics companies for vehicle routing problems (VRP), optimizing delivery routes, and fleet management.
Example: Companies like FedEx or DHL may use routing algorithms to reduce costs and delivery times.
Scheduling and Workforce Optimization:
Solves problems like employee scheduling, shift planning, and resource allocation.
Example: Retail chains optimizing staff schedules to meet customer demand.
Production and Supply Chain:
Multi-modal transportation optimization and production scheduling for manufacturing.
Example: Industrial manufacturers optimizing production processes and transportation routes.
Tech Industry Integration:
OR-Tools is particularly suitable for companies already leveraging Google Cloud or requiring highly customized solutions.
Example: It’s been used by tech companies to optimize infrastructure, such as server allocation in data centers.
Advanced Problem-Solving:
Tackles problems like constraint programming and combinatorial optimization.
Example: Airlines optimizing aircraft crew scheduling or seat allocation.
Industry Adoption
While PuLP and OR-Tools are widely used, proprietary solvers like Gurobi, CPLEX, and FICO Xpress dominate large-scale enterprise-level optimization due to their advanced algorithms, better support, and scalability. However, these tools are expensive and may not be necessary for smaller organizations or academic purposes.
Use Cases for PuLP:
Ideal for industries or teams working on budget constraints, academic research, or small-to-medium-scale problems.
Example: A startup optimizing last-mile delivery routes for a small fleet.
Use Cases for OR-Tools:
Suited for companies handling large-scale and complex problems in logistics, supply chain, and workforce management.
Example: Logistics providers optimizing fleet routes across countries.
How Real-World Adoption Works
Many companies start with open-source tools like PuLP and OR-Tools for proof-of-concept models or as part of a learning curve. If their problem complexity grows, they might migrate to proprietary tools for enhanced performance. However, OR-Tools is robust enough to remain a production-level solution for many large-scale optimization tasks.
What is a Solver?
A solver is a specialized algorithm or software that computes the solution to optimization problems. Once you define the problem (objective function, decision variables, and constraints), the solver performs the heavy lifting to find the optimal solution.
Types of Solvers:
Open-Source Solvers:
Examples: CBC (Coin-or Branch and Cut), GLPK (GNU Linear Programming Kit).
These are free and widely used in academia or smaller-scale problems.
Commercial Solvers:
Examples: Gurobi, IBM CPLEX, FICO Xpress.
These are highly efficient and handle large-scale, complex optimization problems in industries.
Built-in Solvers:
Tools like OR-Tools include their own solvers for linear programming (GLOP) and constraint programming (SAT solver).
How Solvers Work in Optimization
Problem Definition:
You define the problem using a library like PuLP or OR-Tools.
Solver Selection:
The library passes the problem to a solver for computation.
Example: In PuLP, the default solver is CBC, but you can specify others like Gurobi or CPLEX.
Solution:
The solver computes the optimal values for decision variables and returns the result.
What We Learned:
Dispatch Planning: Minimized delivery costs by determining the optimal number of truck trips.
Capacity Optimization: Maximized truck space utilization with selective package loading.
Production Planning: Allocated resources effectively to maximize profit.
Multi-modal Transportation: Minimized transportation costs across multiple transport modes.
By mastering these tools, businesses can streamline operations, enhance decision-making, and achieve cost efficiency in logistics, production, and resource planning. These examples illustrate the transformative power of Operations Research combined with Python.
Next Steps
Ready to apply what you've learned? Here's how you can move forward:
Learn More: Explore Python libraries like PuLP, OR-Tools, and SciPy to master optimization techniques.
Take Action: Experiment with real-world scenarios in logistics, manufacturing, or any industry you're passionate about.
Join the Community: Connect with like-minded professionals and share your progress.
Contact Us: Have questions or need help? Reach out, and let's work together to tackle complex optimization problems.
Optimization starts with action—take the first step today!
For more in-depth technical insights and articles, feel free to explore:
LinkTree: LinkTree - Ebasiq
Substack: ebasiq by Girish
YouTube Channel: Ebasiq YouTube Channel
Instagram: Ebasiq Instagram
Technical Blog: Ebasiq Blog
GitHub Code Repository: Girish GitHub Repos
LinkedIn: Girish LinkedIn
Personal Blog: Girish - BlogBox