Mastering SageMath with Python: A Deep Dive into Symbolic Computation, Graph Theory, and Advanced Mathematics

Explore the Power of SageMath Using Python for Algebra, Graph Visualization, Cryptography, and Scientific Computing – A Comprehensive Guide with Hands-On Examples

What is SageMath?

SageMath, or simply Sage, is an open-source mathematics software system that integrates many existing open-source packages into a unified interface. It is built on top of Python and designed for algebra, geometry, number theory, cryptography, numerical computation, and much more. It provides an alternative to proprietary systems like Mathematica, Maple, and MATLAB.

SageMath can be used interactively via:

• Jupyter Notebooks

• Command-line interface

• Web-based SageMath Cell Server

All the code given here can be tested directly on the Sage Cell Server at https://sagecell.sagemath.org/. Simply copy and paste the code, select the language as Python, and click on the Evaluate button to see the output instantly! 🚀

Additionally, you can use CoCalc at https://cocalc.com/ , a cloud-based platform for SageMath, Jupyter Notebooks, and collaborative mathematical computing. CoCalc provides a more powerful online environment where you can save, share, and work on SageMath projects with advanced features.

Key Features and Capabilities

• Symbolic computation (like SymPy in Python)

• Numerical computation (like NumPy and SciPy)

• Graphing and visualization (like Matplotlib)

• Algebraic geometry and number theory

• Combinatorics and graph theory

• Cryptography applications

• Support for parallel computing

---

Why Use SageMath?

Advantages of SageMath

1. Open-Source & Free: Unlike proprietary alternatives, SageMath is free under the GPL license.

2. Python-based: Uses Python as the core language, making it accessible to Python developers.

3. Integration with Other Libraries: Combines SymPy, NumPy, SciPy, Matplotlib, GAP, Maxima, R, and many other mathematical software packages.

4. Jupyter Notebook Support: Can be used interactively with Jupyter, making it excellent for documentation and visualization.

5. Efficient for Large-scale Computation: Provides multi-threading and parallel computation capabilities.

6. Wide Use Cases: From academic research in algebra to applied machine learning, cryptography, and number theory.

---

Use Cases of SageMath

Try out the SageMath code snippets instantly using Sage Cell Server or explore more with CoCalc.

1. Symbolic Mathematics (Algebra & Calculus)

SageMath can perform algebraic manipulations, simplifications, differentiation, integration, and limits.

Example: Symbolic Computation

from sage.all import *
x = var('x')
f = sin(x)**2 + cos(x)**2
simplified_f = f.trig_reduce()  # Correct trigonometric simplification
print(simplified_f)  # Expected Output: 1

Output:

1

2. Numerical Computation

SageMath supports high-precision numerical computations similar to NumPy and SciPy.

Example: Solving an Equation Numerically

x = var('x')
f = x**3 - 2*x + 1
solution = find_root(f, -2, 2)
print(solution)  # Finds a real root within the range

Output:

-1.6180339887498176

3. Graph Theory & Combinatorics

SageMath has built-in support for graph theory, combinatorics, and discrete mathematics.

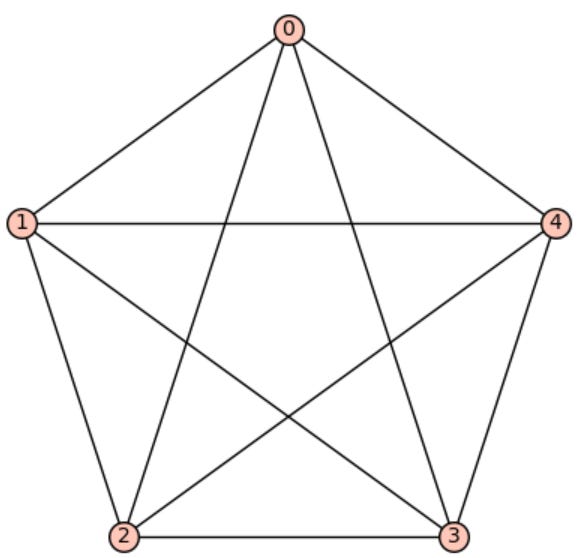
Example: Generating a Graph

G = graphs.CompleteGraph(5)
G.show()

This will display a complete graph with 5 nodes.

Output:

Advanced Graph Visualization

SageMath provides customization options for drawing graphs, such as:

• Coloring vertices and edges

• Labeling nodes and edges

• Specifying layout algorithms (spring, circular, tree, etc.)

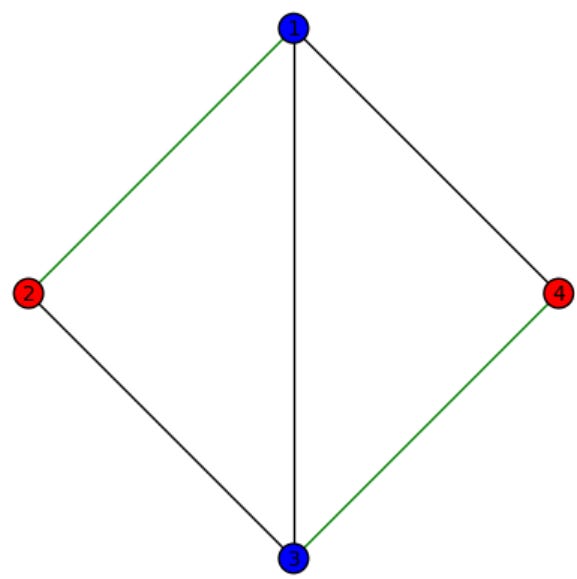
Example: Colored Graph with Custom Layout

G = Graph([(1, 2), (2, 3), (3, 4), (4, 1), (1, 3)])  # Define graph

# Customizing appearance
G.show(
    vertex_colors={'blue': [1, 3], 'red': [2, 4]},
    edge_colors={'green': [(1, 2), (3, 4)]},
    vertex_labels=True,
    layout='circular'
)

Output:

Graph from an Adjacency Matrix

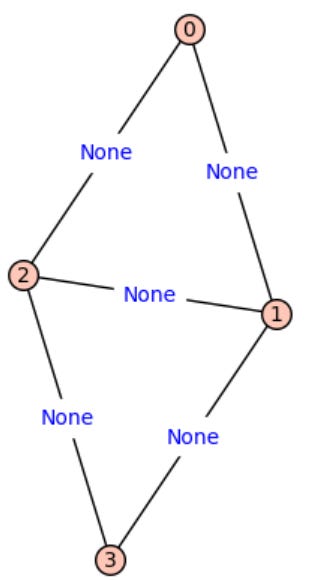
SageMath allows graph creation from matrices, useful for handling network connections and weighted graphs.

Example: Creating a Graph from an Adjacency Matrix

M = Matrix([
    [0, 1, 1, 0],
    [1, 0, 1, 1],
    [1, 1, 0, 1],
    [0, 1, 1, 0]
])
G = Graph(M)
G.show(vertex_labels=True, edge_labels=True)CopyEdit

Output:

Weighted Graphs & Edge Labels

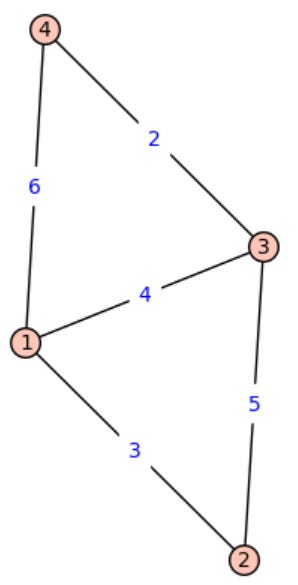
A weighted graph assigns a numerical weight to each edge.

Example: Weighted Graph

G = Graph()
G.add_edges([(1, 2, 3), (2, 3, 5), (3, 4, 2), (4, 1, 6), (1, 3, 4)])

# Show graph with edge weights
G.show(edge_labels=True, layout='spring')

Output:

Generating Random Graphs

SageMath allows random graph generation, useful for modeling real-world networks.

Example: Generating a Random Graph (Erdős–Rényi Model)

G = graphs.RandomGNP(10, 0.3)  # 10 nodes, 30% probability of connection
G.show(layout="spring")

Output:

4. Cryptography

SageMath is extensively used in modern cryptography research.

Example: RSA Key Generation

p = random_prime(2^128)
q = random_prime(2^128)
n = p * q
phi = (p - 1) * (q - 1)
e = 65537  # Common choice
d = inverse_mod(e, phi)
print(f"Public Key: ({n}, {e})")
print(f"Private Key: {d}")

Output:

Public Key: (2407, 65537)
Private Key: 1489

5. Linear Algebra

Matrix operations, eigenvalues, and solving linear systems are simple in SageMath.

Example: Solving a Linear System

A = Matrix([[2, 1], [1, 3]])
b = vector([8, 13])
solution = A.solve_right(b)
print(solution)  # Solves Ax = b

Output:

(11/5, 18/5)

6. Differential Equations

SageMath can solve both ordinary and partial differential equations.

Example: Solving a Differential Equation

from sage.all import *
t = var('t')  # Declare independent variable
y = function('y')(t)  # Declare dependent variable as a function of t

de = diff(y, t) - y  # Define the differential equation dy/dt = y
sol = desolve(de, y)  # Solve the equation
print(sol)  # Expected solution: c*e^t

Output:

_C*e^t

7. Machine Learning & Data Analysis

While not designed specifically for machine learning, SageMath can work with Python's ML libraries like TensorFlow, PyTorch, and Scikit-learn.

Example: Basic Data Analysis with SageMath

import pandas as pd
import numpy as np

data = pd.DataFrame({'A': np.random.rand(5), 'B': np.random.rand(5)})
print(data.describe())  # Quick statistical summary

Output:

              A         B
count  5.000000  5.000000
mean   0.452136  0.604130
std    0.193276  0.269582
min    0.218184  0.246191
25%    0.270156  0.426962
50%    0.560503  0.647458
75%    0.570344  0.785257
max    0.641491  0.914781

8. AES (Advanced Encryption Standard) Implementation in SageMath

AES (Advanced Encryption Standard) is one of the most widely used symmetric encryption algorithms. It operates on fixed-size 128-bit blocks using key sizes of 128, 192, or 256 bits. SageMath supports finite field arithmetic, which is essential for understanding AES internals.

Example: AES S-Box (Substitution Box) Computation in SageMath

The AES S-Box is a crucial component in the AES encryption process. It performs byte substitution using finite field inversion and an affine transformation.

# Define the AES finite field GF(2^8) using the AES standard polynomial modulus
AES_field = GF(2**8, name='x', modulus=x**8 + x**4 + x**3 + x + 1)

# Compute AES S-Box using the inverse in the finite field
AES_Sbox = {}
for i in range(256):
    element = AES_field(i)  # Convert i into a finite field element
    if element == 0:
        AES_Sbox[i] = 0  # AES defines the inverse of 0 as 0
    else:
        AES_Sbox[i] = element.inverse()  # Compute multiplicative inverse in GF(2^8)

# Print first 16 values of S-Box
print("AES S-Box (First 16 values):", [AES_Sbox[i] for i in range(16)])

Output:

AES S-Box (First 16 values): [0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1]

Key Concepts in This Example:

✅ AES Finite Field Arithmetic – AES operates in GF(2⁸) using a specific polynomial modulus.
✅ AES S-Box Computation – Uses the inverse in GF(2⁸) to enhance security against linear & differential cryptanalysis.
✅ Byte Substitution – A non-linear transformation in AES encryption to add confusion.

Use Cases of AES in Cryptography:

• Secure Communications – Used in SSL/TLS, VPNs, and HTTPS encryption.

• Disk Encryption – Protects BitLocker (Windows), FileVault (macOS), and LUKS (Linux).

• Wi-Fi Security (WPA2/WPA3) – AES is used in Wi-Fi encryption protocols.

SageMath allows researchers and security enthusiasts to explore AES internals, including S-Box, key expansion, and MixColumns transformations!

How to Use SageMath?

You can use SageMath Cloud (CoCalc) for an online experience without installation.

https://sagecell.sagemath.org/

Stay tuned for the installation guide in the upcoming article, where I will deep dive into setting up SageMath on different platforms like Windows, Mac and Linux!

When to Use SageMath?

• If you need a unified platform for symbolic and numerical computation.

• When working on mathematical research that involves algebra, number theory, or cryptography.

• For graph theory and combinatorics without installing multiple separate Python libraries.

• If you prefer a Mathematica-like experience using Python.

However, if you are primarily working with data science and machine learning, sticking with NumPy, SciPy, and TensorFlow might be a better choice.

Conclusion

SageMath is a comprehensive and powerful mathematical computing system that integrates symbolic computation, numerical analysis, graph theory, cryptography, and more. It provides:

✅ Multi-platform availability – Works best on Linux/macOS via Homebrew, APT, or Conda; Windows users should use WSL or CoCalc.
✅ Advanced algebraic capabilities – Supports polynomial algebra, Groebner bases, and symbolic computation.
✅ Graph visualization & network analysis – Easily creates graphs, adjacency matrices, and computes shortest paths, Eulerian & Hamiltonian circuits, and PageRank.
✅ Integration with Jupyter Notebook – Enables an interactive coding experience for education and research.
✅ High-performance computing – Leverages Cython and parallel processing for complex computations.
✅ Flexible scripting & mathematical modeling – Can be used for cryptography, quantum computing simulations, AI research, and mathematical proofs.

With its open-source nature and Python-based interface, SageMath serves as a powerful alternative to proprietary tools like Mathematica and MATLAB, making it ideal for researchers, educators, and students alike.

---

For more in-depth technical insights and articles, feel free to explore:

Girish Central

• LinkTree: GirishHub – A single hub for all my content, resources, and online presence.

• LinkedIn: Girish LinkedIn – Connect with me for professional insights, updates, and networking.

Ebasiq

• Substack: ebasiq by Girish – In-depth articles on AI, Python, and technology trends.

• Technical Blog: Ebasiq Blog – Dive into technical guides and coding tutorials.

• GitHub Code Repository: Girish GitHub Repos – Access practical Python, AI/ML, Full Stack and coding examples.

• YouTube Channel: Ebasiq YouTube Channel – Watch tutorials and tech videos to enhance your skills.

• Instagram: Ebasiq Instagram – Follow for quick tips, updates, and engaging tech content.

GirishBlogBox

• Substack: Girish BlogBlox – Thought-provoking articles and personal reflections.

• Personal Blog: Girish - BlogBox – A mix of personal stories, experiences, and insights.

Ganitham Guru

• Substack: Ganitham Guru – Explore the beauty of Vedic mathematics, Ancient Mathematics, Modern Mathematics and beyond.

• Mathematics Blog: Ganitham Guru – Simplified mathematics concepts and tips for learners.