Demystifying Data Structures, Sorting Algorithms, and Big O Complexity — A Complete Beginner’s Guide

From understanding how data is organized and sorted to mastering time and space complexity, this guide breaks down core DSA concepts using real-world analogies, code examples, and practical use cases.

What is Data Structures and Algorithms?

Data Structures and Algorithms (DSA) is a combined term used in computer science and programming that refers to two fundamental concepts:

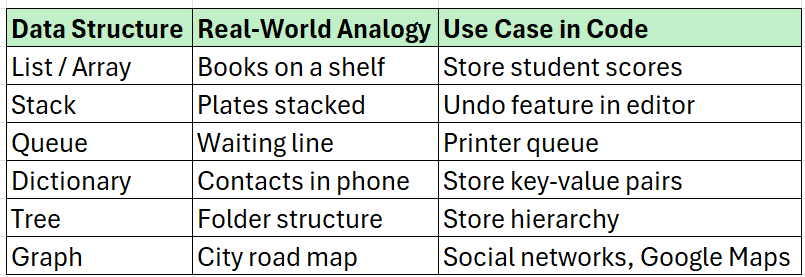
Data Structures - How Do We Store Data?

Definition:
A data structure is a way of organizing and storing data in a computer so that it can be accessed and modified efficiently.

Example:
Imagine you're running a library.

You have books, and you can choose to store them in different ways:

• On shelves in a row → like an Array or List

• One over the other → like a Stack

• Queue at the counter → like a Queue

• By category or author → like a Dictionary or HashMap

• A branching catalog of books → like a Tree

• Books linked to related books → like a Graph

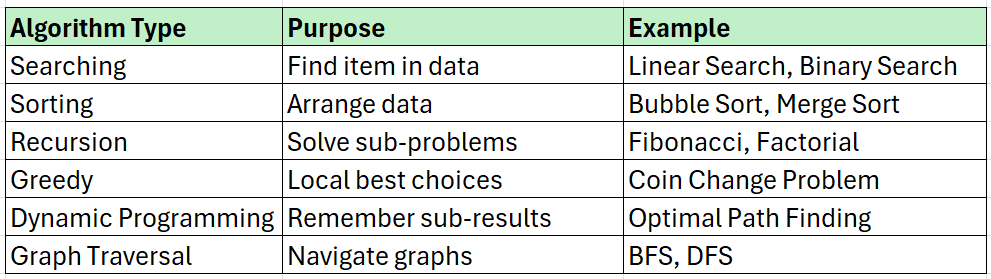
Algorithms - How Do We Process Data?

Definition:
An algorithm is a step-by-step procedure or formula to solve a problem.

Example:
If you want to make a cup of tea, the steps like boiling water, adding tea leaves, pouring into a cup, etc., form an algorithm.

In programming, if you want to find a number in a list, you can:

• Check one by one → Linear Search (Simple Algorithm)

• Use divide-and-conquer → Binary Search (Efficient Algorithm for sorted lists)

For the stored books in the library (data), you need to:

• Find a specific book → Search Algorithm

• Sort books by title → Sorting Algorithm

• Recommend books based on category → Recommendation Algorithm

Why Data Structures and Algorithms Together?

Because solving a problem efficiently requires both:

"Right Data Structure + Right Algorithm = Optimal Solution"

For example:

• Finding the shortest route in Google Maps?

  • Data Structure: Graph

  • Algorithm: Dijkstra’s Algorithm

• Back button in browser?

  • Data Structure: Stack

  • Algorithm: Push and Pop operations

Example in Python

# Problem: Find the maximum number in a list

# Data Structure: List (to store numbers)
numbers = [10, 4, 23, 78, 5]

# Algorithm: Traverse the list and find the maximum
max_num = numbers[0]
for num in numbers:
    if num > max_num:
        max_num = num

print("Maximum number is:", max_num)

Breakdown:

• ✅ List is the data structure used to store the numbers.

• ✅ The loop is the algorithm used to find the max value.

Why Is DSA Important?

• 📱 Used in mobile apps, websites, games, AI, databases

• 💼 Crucial for interviews (Amazon, Google, Microsoft)

• ⚙️ Improves performance and memory usage

• 🧠 Enhances logical and problem-solving skills

Summary

Data Structures (DS): How you store and organize your data.
Algorithms (A): How you process and manipulate that data to solve a problem.

What is Sorting?

Sorting is the process of arranging data in a particular order — usually ascending (1, 2, 3…) or descending (9, 8, 7…).

Where is Sorting Used?

Sorting is mostly applied on Arrays (or Lists in Python).
However, you can also sort:

• Linked Lists

• Files or records (in databases)

• Strings and other collections

✅ Primary Data Structure for Sorting: Array / List

Why Sorting?

• Speeds up searching (like Binary Search requires sorted data)

• Organizes data for reporting

• Essential in ranking, scheduling, and recommendation systems

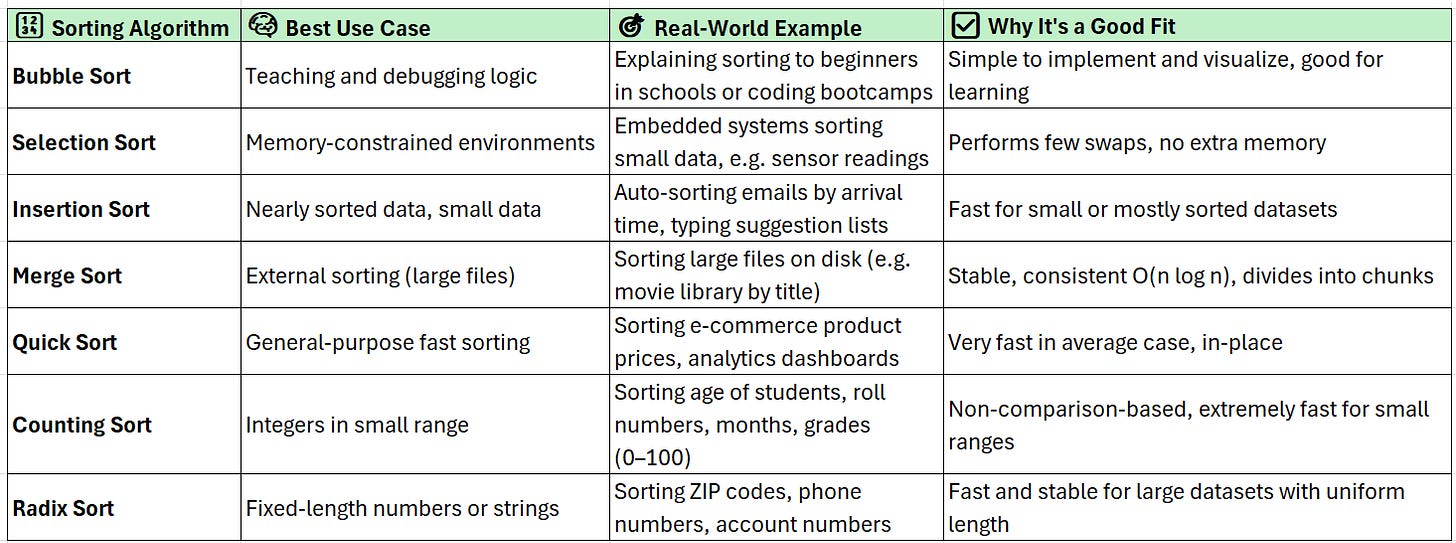
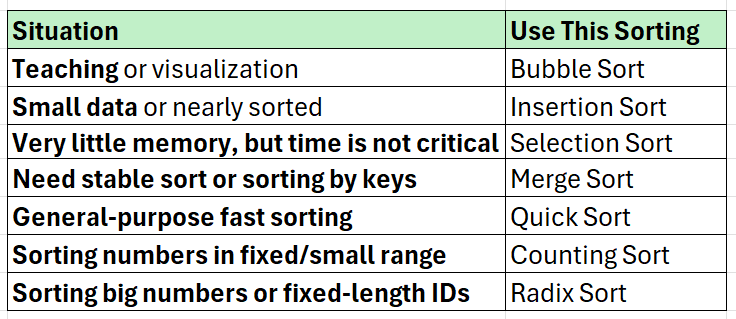
Types of Sorting Algorithms

1. Bubble Sort (Simple but slow)

Concept: Repeatedly compare adjacent elements and swap if they are in the wrong order.

Python Code:

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):  # Repeat passes
        for j in range(0, n-i-1):  # Inner loop reduces every pass
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]  # Swap
    return arr

print(bubble_sort([5, 1, 4, 2, 8]))

🧠 Use Case: Simple cases, teaching concept
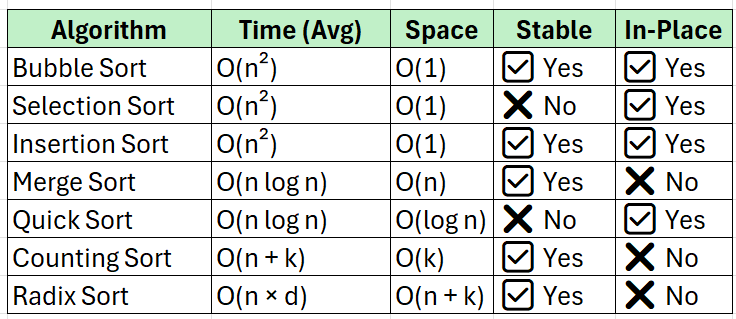
🕒 Time: O(n²)

2. Selection Sort (Select and Place)

Concept: Find the minimum element and place it at the beginning. Repeat for remaining list.

Python Code:

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_index = i
        for j in range(i+1, n):  # Find minimum in remaining list
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]  # Swap
    return arr

print(selection_sort([5, 1, 4, 2, 8]))

🧠 Use Case: Simple logic, less swaps
🕒 Time: O(n²)

3. Insertion Sort (Insert in order)

Concept: Build sorted list one by one by inserting elements at the correct place.

Python Code:

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        # Move elements greater than key
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

print(insertion_sort([5, 1, 4, 2, 8]))

🧠 Use Case: Small lists, nearly sorted
🕒 Time: O(n²)

4. Merge Sort (Divide and Conquer)

Concept: Split array into halves, sort each half, then merge them.

Python Code:

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        # Merge sorted halves
        i = j = k = 0
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        # Copy leftovers
        while i < len(L):
            arr[k] = L[i]
            i += 1; k += 1
        while j < len(R):
            arr[k] = R[j]
            j += 1; k += 1

    return arr

print(merge_sort([5, 1, 4, 2, 8]))

🧠 Use Case: Large datasets, stable sort
🕒 Time: O(n log n)

5. Quick Sort (Fast Divide and Conquer)

Concept: Pick a pivot, partition the array into smaller and larger elements, recursively sort them.

Python Code:

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[0]
    less = [x for x in arr[1:] if x <= pivot]
    greater = [x for x in arr[1:] if x > pivot]
    return quick_sort(less) + [pivot] + quick_sort(greater)

print(quick_sort([5, 1, 4, 2, 8]))

🧠 Use Case: Fastest average case
🕒 Time: Avg: O(n log n), Worst: O(n²)

6. Built-in Sort (Python sort() or sorted())

arr = [5, 1, 4, 2, 8]
arr.sort()
print(arr)
# OR
print(sorted([5, 1, 4, 2, 8]))

🧠 Python uses TimSort (Hybrid of Merge + Insertion Sort)
🕒 Time: O(n log n) in practice

7. Counting Sort — Frequency-Based Sorting

Concept:

• Counting Sort works by counting the number of occurrences of each element.

• Then it places elements directly into their correct position using these counts.

When to Use:

• You know the range of values (like 0 to 100).

• All elements are non-negative integers (works best here).

Steps:

1. Find the maximum value in the array.

2. Create a count[] array to store frequency of each number.

3. Modify count[] to store positions.

4. Build the output array using count[].

Python Code:

def counting_sort(arr):
    max_val = max(arr)
    count = [0] * (max_val + 1)

    # Step 1: Count occurrences
    for num in arr:
        count[num] += 1

    # Step 2: Modify count to hold positions
    for i in range(1, len(count)):
        count[i] += count[i - 1]

    # Step 3: Build output array
    output = [0] * len(arr)
    for num in reversed(arr):
        output[count[num] - 1] = num
        count[num] -= 1

    return output

print(counting_sort([4, 2, 2, 8, 3, 3, 1]))

Time Complexity:

• Best / Average / Worst: O(n + k)
  (n = size of input, k = max element)

• Space: O(k)

✅ Stable: Yes

✅ Non-Comparative: Yes

8. Radix Sort — Digit-by-Digit Sorting

Concept:

• Radix Sort sorts integers digit by digit, starting from least significant digit (LSD).

• It uses a stable sort (usually Counting Sort) at each digit level.

When to Use:

• Integers or strings of fixed length.

• You want better than O(n log n) time for large integer data.

Steps:

1. Find the maximum number to know the number of digits.

2. Sort all numbers based on each digit, from least significant to most significant.

3. Use a stable sort like Counting Sort at each digit level.

Python Code:

def counting_sort_for_radix(arr, exp):
    n = len(arr)
    output = [0] * n
    count = [0] * 10  # Digits 0-9

    # Count digit frequency
    for i in range(n):
        index = (arr[i] // exp) % 10
        count[index] += 1

    # Modify count
    for i in range(1, 10):
        count[i] += count[i - 1]

    # Build output
    for i in reversed(range(n)):
        index = (arr[i] // exp) % 10
        output[count[index] - 1] = arr[i]
        count[index] -= 1

    return output

def radix_sort(arr):
    max_val = max(arr)
    exp = 1
    while max_val // exp > 0:
        arr = counting_sort_for_radix(arr, exp)
        exp *= 10
    return arr

print(radix_sort([170, 45, 75, 90, 802, 24, 2, 66]))

Time Complexity:

• Best / Avg / Worst: O(n * d)
  (n = number of elements, d = number of digits)

• Space: O(n + k) per pass

Stable: Yes

Non-Comparative: Yes

Summary

Use cases for all Algorithms

Use Case: A School System

Let’s say you’re building a school management system. Here's how different sorts could help:

Memory and Time Complexity Quick Reference

Final Takeaways — How to Choose the Right Sort

---

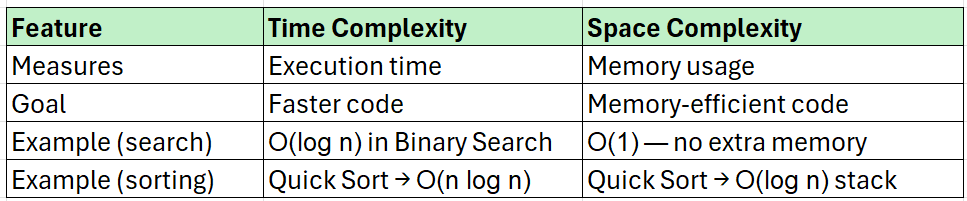
What is Time and Memory Complexity?

When you write code, you want to know:

• How fast is it? → Time Complexity

• How much memory it uses? → Space (Memory) Complexity

These are measured using Big O Notation like O(n), O(log n), O(n²), etc.

Time Complexity: How Fast Does My Code Run?

Definition:

Time complexity tells you how the runtime of your algorithm increases as the size of the input grows.

Analogy:

Imagine you're searching for a name in a phonebook with 1000 pages.

• Go page-by-page (linear) → O(n)

• Open to middle, then divide again (binary) → O(log n)

Simple Example

def print_items(arr):
    for item in arr:
        print(item)

If the list arr has:

• 10 items → 10 steps

• 1000 items → 1000 steps

🧠 Time Complexity = O(n)
(n = number of items)

Common Time Complexities

Space (Memory) Complexity: How Much Memory is Used?

Definition:

Space complexity measures how much additional memory your algorithm uses based on input size.

Analogy:

Think of a backpack. If you add more books (data), your bag (memory) gets heavier. Some methods need more space to process data.

Simple Example:

def create_list(n):
    new_list = []
    for i in range(n):
        new_list.append(i)
    return new_list

This function creates a new list of size n, so:

• Space increases linearly → O(n)

Common Space Complexities

Difference Between Time and Space Complexity

Combined Example

def sum_list(arr):
    total = 0           # O(1) space
    for num in arr:     # O(n) time
        total += num
    return total

• Time Complexity = O(n) (we loop through all items)

• Space Complexity = O(1) (we use just one variable total)

Final Tip

When analyzing an algorithm:

1. Check how many operations grow with input → Time.

2. Check how many extra variables/data structures are created → Space.

Conclusion

Wrapping It All Together — Think Logically, Code Smartly

Data Structures and Algorithms form the foundation of computer science — they’re the tools that turn logic into power. By understanding different data structures and choosing the right algorithm, you can solve real-world problems more efficiently and elegantly.

Whether you're:

• Picking between Bubble Sort or Quick Sort,

• Sorting student records or zip codes,

• Or wondering whether to optimize for speed or memory…

The key is not just writing working code, but writing smart, scalable code.

Learn to ask:

• “What structure fits my data?”

• “Which algorithm scales better?”

• “Can I trade memory for speed or vice versa?”

By mastering these basics — Sorting + Time + Space + Use Cases — you're not only preparing for interviews or exams, but also training your mind to think like an engineer.

---

For more in-depth technical insights and articles, feel free to explore:

Girish Central

• LinkTree: GirishHub – A single hub for all my content, resources, and online presence.

• LinkedIn: Girish LinkedIn – Connect with me for professional insights, updates, and networking.

Ebasiq

• Substack: ebasiq by Girish – In-depth articles on AI, Python, and technology trends.

• Technical Blog: Ebasiq Blog – Dive into technical guides and coding tutorials.

• GitHub Code Repository: Girish GitHub Repos – Access practical Python, AI/ML, Full Stack and coding examples.

• YouTube Channel: Ebasiq YouTube Channel – Watch tutorials and tech videos to enhance your skills.

• Instagram: Ebasiq Instagram – Follow for quick tips, updates, and engaging tech content.

GirishBlogBox

• Substack: Girish BlogBlox – Thought-provoking articles and personal reflections.

• Personal Blog: Girish - BlogBox – A mix of personal stories, experiences, and insights.

Ganitham Guru

• Substack: Ganitham Guru – Explore the beauty of Vedic mathematics, Ancient Mathematics, Modern Mathematics and beyond.

• Mathematics Blog: Ganitham Guru – Simplified mathematics concepts and tips for learners.